分类变量是指取值属于有限、通常是非数值类别的变量。在数据分析和机器学习中,分类变量广泛存在,如性别(男性、女性、其他)、颜色(红色、蓝色、绿色等)、教育水平(高中、本科、研究生等)。由于大多数机器学习算法无法直接处理非数值数据,因此需要对分类变量进行特殊处理,将其转换为算法可接受的数值形式。
继续阅读分类目录归档:机器学习
scikit-learn的CART树——寻找分裂点的两种模式|使用技巧
CART树
CART(Classification and Regression Trees)是一种用于分类和回归任务的决策树算法。它通过选择最优特征和分裂点来构建树结构,能够有效地对数据进行分类或预测。
两种模式
CART树在寻找最佳分裂点时主要有两种模式:完全遍历模式和部分遍历模式。
继续阅读scikit-learn中的树算法 不能直接使用分类变量
scikit-learn中的算法都不直接支持分类变量
不只是scikit-learn中的树算法不能直接使用分类变量,scikit-learn中的算法都不直接支持分类变量。在使用这些算法之前,需要将分类变量转换为独热编码(one-hot)或整数类型。
继续阅读CART决策树算法:如何处理数值型与分类型特征
CART算法
决策树是一种非参数的监督学习方法,它不对数据集的分布形式做任何具体假设,但会根据数据中的特征类型和标签值动态地生成模型结构可以用于分类和回归问题。决策树的核心思想是递归地将特征空间划分为若干个单元,使得每个单元内的样本尽可能同质(即属于同一类别或具有相似的目标值)。
继续阅读特征是什么
决策树算法的编程实现——递归的用法
决策树是一种常用的机器学习算法,广泛应用于分类和回归任务中。递归在决策树的实现中起着至关重要的作用,通过递归调用,可以有效地构建和使用决策树。本文将详细介绍决策树实现算法中的递归,重点讲解基线条件与递归调用的实现。
继续阅读最小描述长度原理 | 机器学习的基础
[latexpage]
最小描述长度:一个美丽的想法,它将统计学、信息论和哲学的概念结合在一起,为机器学习奠定了基础。
最小描述长度(MDL)的概念
最小描述长度(Minimum Description Length, MDL)原理是一种基于信息论的方法,用于解决模型选择和数据压缩问题。它是由Jorma Rissanen在1978年开始的⼀系列论⽂中提出的。
标准化与规范化之间的选择 | 数据预处理的关键
标准化(Standardization)与规范化(Normalization), 有何不同?
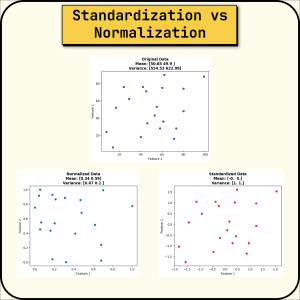
规范化(Normalization)
也称“归一化”,它将值重新缩放到 [0,1] 范围内。 它也被称为最小-最大缩放。
如果您希望不同的数据集处于相同的正比例上,这将非常有用。 它还为值创建了一个边界。
从“预测明天下雨的概率”说频率学派与贝叶斯学派
要计算天气事件这一非重复性质的单次事件的概率,我们通常不能直接应用频率主义学派的方法。相反,需要运用基于统计模型和当前环境数据的方法进行概率的估算。
频率主义学派的理论与解释局限性
频率主义学派认为,概率是大量相同条件下事件发生的长期频率。因此,对于无法重复实验验证的单个事件,如“明天下雨”这一预测,频率主义学派的理论并不适用。
柯尔莫戈洛夫复杂性(Kolmogorov Complexity)理论
定义
柯尔莫戈洛夫复杂性(Kolmogorov Complexity),是衡量一个对象信息内容大小的一种方法,它通过寻找描述该对象最短的二进制程序长度来定义。具体来说,一个对象的柯尔莫戈洛夫复杂性是指在给定的计算模型下,能够生成该对象的最短程序的长度。这个定义提供了一种量化对象信息量的方式,不依赖于具体的编码方式。